Abstract:
A discrete strategy improvement algorithm is given for
constructing winning strategies in parity games, thereby providing also a new
solution of the model-checking problem for the modal 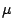 -calculus. Known
strategy improvement algorithms, as proposed for stochastic games by Hoffman
and Karp in 1966, and for discounted payoff games and parity games by Puri in
1995, work with real numbers and require solving linear programming instances
involving high precision arithmetic. In the present algorithm for parity
games these difficulties are avoided by the use of discrete vertex valuations
in which information about the relevance of vertices and certain distances is
coded. An efficient implementation is given for a strategy improvement step.
Another advantage of the present approach is that it provides a better
conceptual understanding and easier analysis of strategy improvement
algorithms for parity games. However, so far it is not known whether the
present algorithm works in polynomial time. The long standing problem whether
parity games can be solved in polynomial time remains open
-calculus. Known
strategy improvement algorithms, as proposed for stochastic games by Hoffman
and Karp in 1966, and for discounted payoff games and parity games by Puri in
1995, work with real numbers and require solving linear programming instances
involving high precision arithmetic. In the present algorithm for parity
games these difficulties are avoided by the use of discrete vertex valuations
in which information about the relevance of vertices and certain distances is
coded. An efficient implementation is given for a strategy improvement step.
Another advantage of the present approach is that it provides a better
conceptual understanding and easier analysis of strategy improvement
algorithms for parity games. However, so far it is not known whether the
present algorithm works in polynomial time. The long standing problem whether
parity games can be solved in polynomial time remains open
Available as PostScript, PDF, DVI.