Recent Advances in -definability over Continuous Data Types

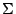
The purpose of this paper is to survey our recent research in computability and definability over continuous data types such as the real numbers, real-valued functions and functionals. We investigate the expressive power and algorithmic properties of the language of $\Sigma$ -formulas intended to represent computability over the real numbers. In order to adequately represent computability we extend the reals by the structure of hereditarily finite sets. In this setting it is crucial to consider the real numbers without equality since the equality test is undecidable over the reals. 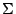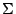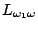We prove Engeler's Lemma for $\Sigma$ -definability over the reals without the equality test which relates $\Sigma$ -definability with definability in the constructive infinitary language $L_{\omega_1 \omega}$ . 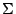Thus, a relation over the real numbers is $\Sigma$ -definable if and only if it is definable by a disjunction of a recursively enumerable set of quantifier free formulas. 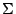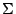This result reveals computational aspects of $\Sigma$ -definability and also gives topological characterisation of $\Sigma$ -definable relations over the reals without the equality test. 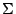We also illustrate how computability over the real numbers can be expressed in the language of $\Sigma$ -formulas

Abstract: